
Publications | Talks | Teaching | CV
E-Mail |
ORCiD |
GitLab (university) |
GitLab (personal) |
GitHub |
Bluesky |
Mastodon |
![]() Linkedin |
Linkedin |
![]() YouTube
YouTube
joint work with Tobias Harks and Julian Schwarz
A social optimal dynamic flow is a dynamic flow minimizing the sum of all particles' travel time. For such flows we study the question of whether one can always find time-dependent tolls which turn the given flow into a dynamic equilibrium (when particles aim to minimize a weighted sum of travel time and tolls along their chosen route).
For multi-source multi-destination networks it turns out that there are instances where no social optimal flow can be implemented as equilibrium using tolls. In single-source single-destination networks, on the other hand, every social optimum can be implemented (assuming certain monotonicity assumptions on the flow dynamics).
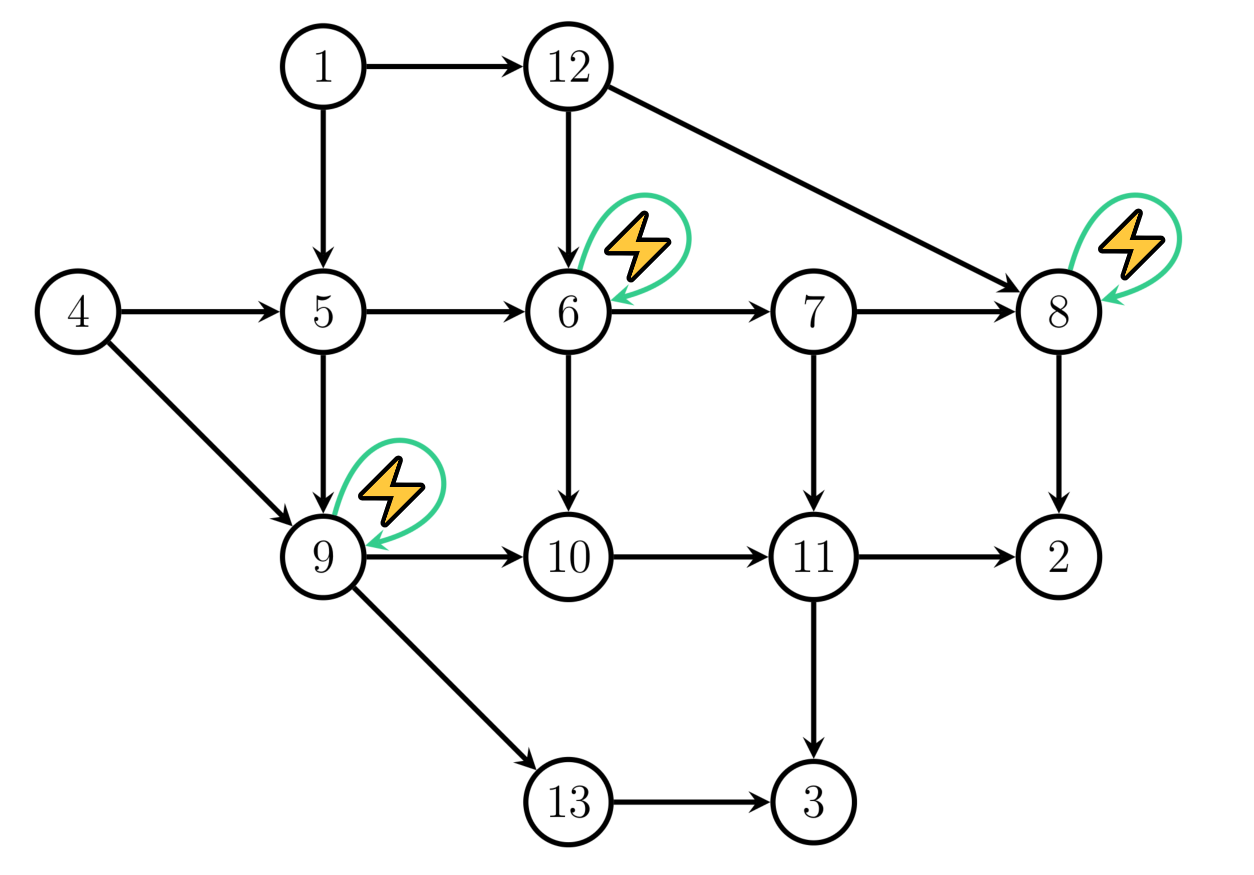
joint work with Tobias Harks and Prashant Palkar
We study dynamic traffic assignment for electrical vehicles addressing the specific challenges such as range limitations and the possibility of battery recharge at predefined charging locations. We pose the dynamic equilibrium problem within the deterministic queueing model of Vickrey and as our main result, we establish the existence of an energy-feasible dynamic equilibrium. We complement our theoretical results by a computational study in which we design a fixed-point algorithm computing energy-feasible dynamic equilibria.
Talk slides: ATMOS 2022, Dagstuhl-Seminar
joint work with Tobias Harks and Julian Schwarz
We study the question for which dynamic flows one can find tolls on the edges such that the flow becomes an equilibrium flow with respect to the weighted sum of travel times and tolls. We give a complete characterization of those flows (for the case of multiple commodities with different value-of-time parameter but same origin and destination):
Namely, a dynamic flow can be implemented via tolls if and only if the subgraph of used edges never contains a cycles of strictly positive travel time which also contains the destination.
Related material: Errata
joint work with Tobias Harks and Michael Markl
We propose a general framework for DTA which includes both descriptive and prescriptive models. The framework can be instantiated with an edge loading operator mapping edge inflow rates to edge outflow rates (hence, representing the physical aspect of the model) and a routing operator mapping flows to sets of allowed flow splits at the nodes (therefore, representing the behavioural aspect of the model). In this way the framework includes both known models (like full information or instantaneous dynamic equilibria) as well as new models like prediction equilibria with random measurement errors.
In this paper we derive several sufficient conditions for existence and uniqueness of flows adhering to a given pair of edge loading and routing operator.
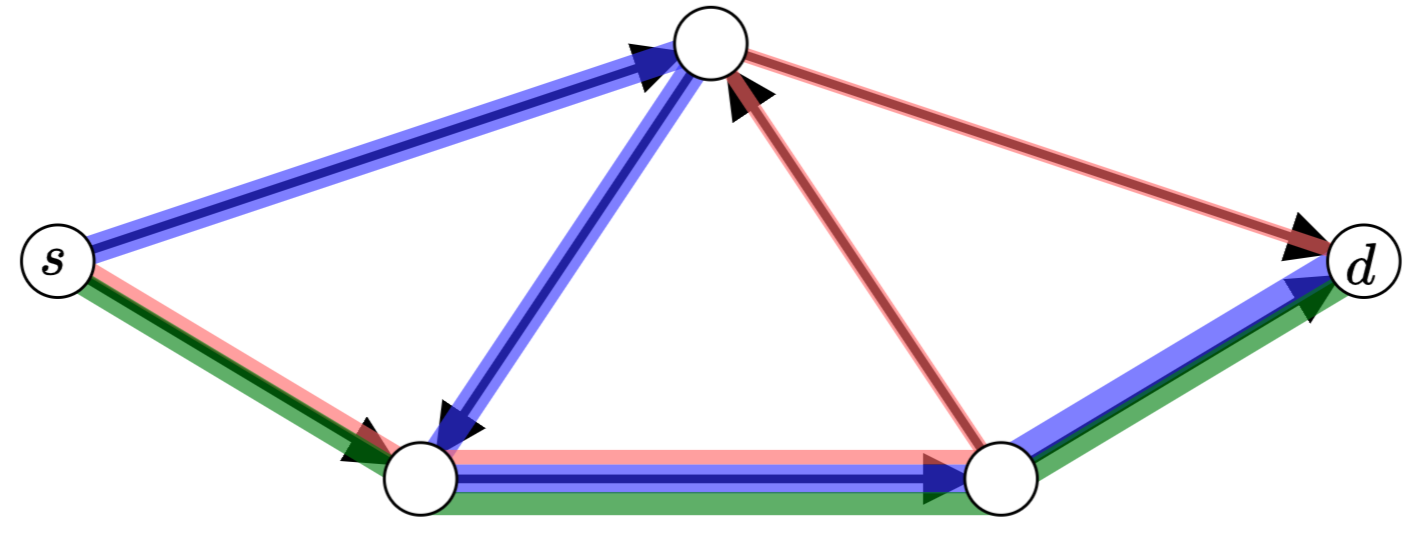
This thesis studies dynamic flows comprised of infinitesimally small agents (=flow particles) travelling through a network while continuously adapting their choice of route based on the current state of the network as determined by the flow up to the current time. More, precisely, we study dynamic flows in networks with deterministic queueing wherein particles only ever enter edges which lie on currently shortest paths towards their destination and call the resulting equilibrium states instantaneous dynamic equilibria (IDE).
After the introduction of the formal model, the main topics of this thesis are existence, computation and quality of IDE.
Talk slides: OR 2024, DCGT 2024, Thesis Defense, Group workshop, Graduate Get Together
Related material: Poster, Summary for the general public (GOR Blog, German), Errata
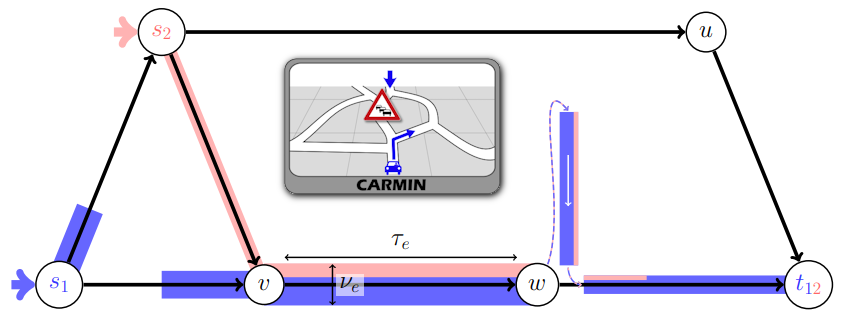
joint work with Tobias Harks
We study dynamic traffic assignment with side-constraints. We first give a counter-example to a key result from the literature regarding the existence of dynamic equilibria for volume-constrained traffic models in the classical edge-delay model. We then propose a new framework for side-constrained dynamic equilibria based on the concept of feasible ε-deviations of flow particles in space and time. Under natural assumptions, we characterize the resulting equilibria by means of quasi-variational and variational inequalities, respectively. Finally, we establish first existence results for side-constrained dynamic equilibria for the non-convex setting of volume-constraints.
Related material: Errata
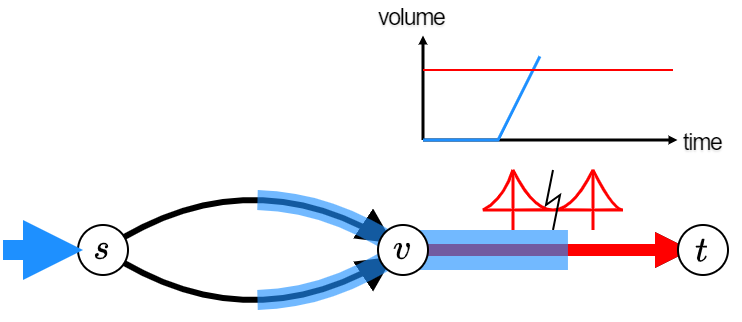
joint work with Tobias Harks and Julian Schwarz
We study the decomposition problem for the setting of dynamic s,d-flows under a general flow propagation model. We prove that any dynamic edge s,d-flow with bounded support can be decomposed into a linear combination of inflows into s,d-walks and zero-cycles. To this goal we show that a variant of the classical algorithmic approach of iteratively subtracting walk inflows from the current dynamic edge flow converges to a dynamic circulation. We further characterize those dynamic edge flows that allow a decomposition using only walk inflows.
Talk slides: Dagstuhl Seminar
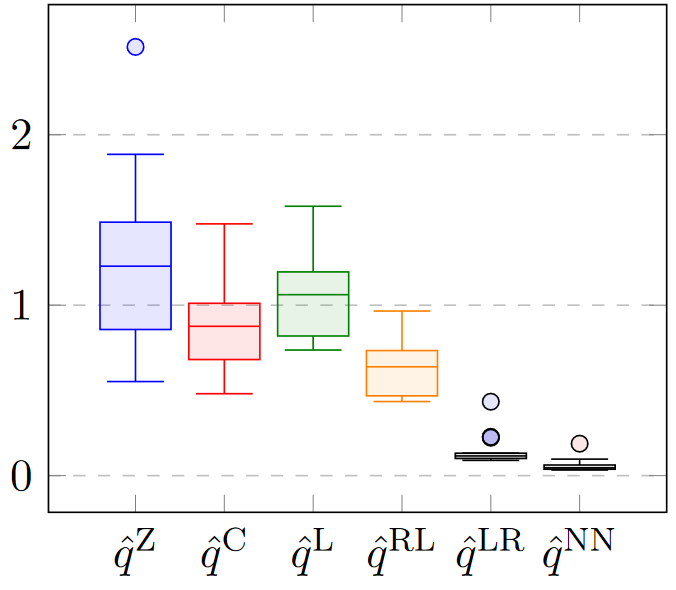
joint work with Tobias Harks, Kostas Kollias and Michael Markl
We study a dynamic traffic assignment model, where agents base their instantaneous routing decisions on real-time delay predictions. We describe a general mathematical model which, in particular, includes the settings leading to IDE und DE. On the theoretical side we show existence of equilibrium solutions under some additional assumptions while on the practical side we implement a machine-learned predictor and compare it to other static predictors.
Related material: Code
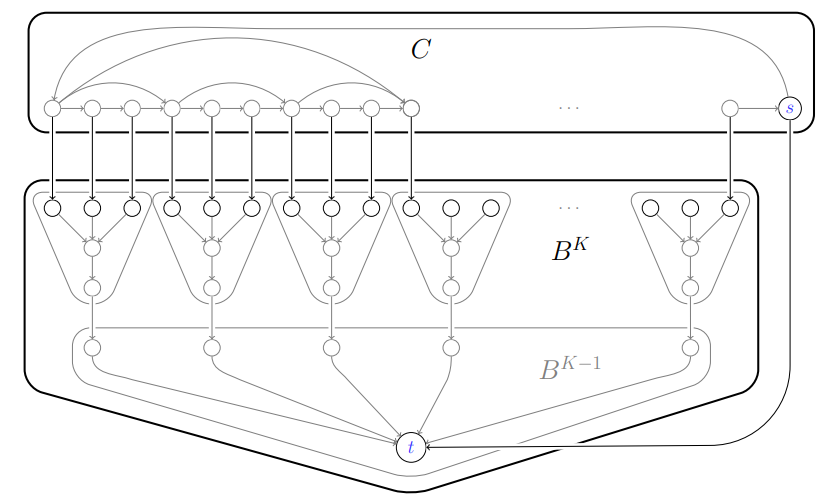
joint work with Tobias Harks
We study the price of anarchy (PoA) for Instantaneous Dynamic Equilibria (IDE) and show an upper bound of order O(U⋅τ) for single-sink instances, where U denotes the total inflow volume and τ the sum of edge travel times. We complement this upper bound with a family of instances proving a lower bound of order Ω(U⋅logτ).
Talk slides: WINE 2020, OR 2019
Related material: Errata
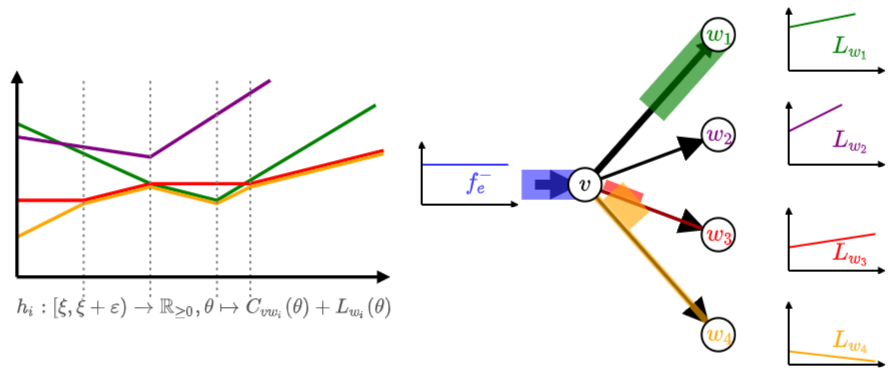
joint work with Tobias Harks
We study the computational complexity of Instantaneous Dynamic Equilibria (IDE) and show that a natural extension algorithm needs only finitely many phases to converge leading to the first finite time combinatorial algorithm computing an IDE. We complement this result by several hardness results showing that computing IDE with natural properties is NP-hard.
Talk slides: IPCO 2021, Dagstuhl-Seminar
Related material: Errata
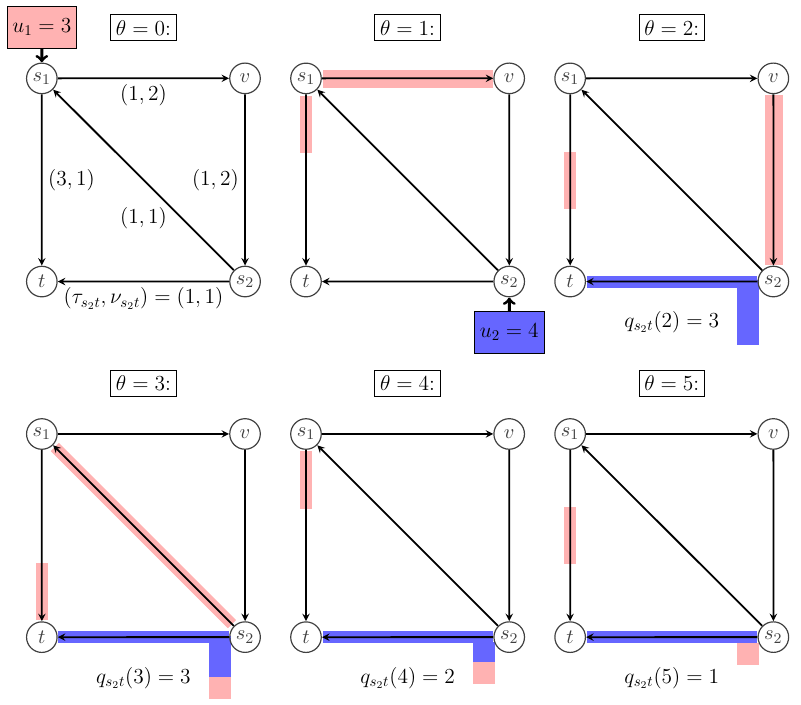
joint work with Tobias Harks and Leon Sering
We study dynamic network flows and introduce a notion of instantaneous dynamic equilibrium (IDE) requiring that for any positive inflow into an edge, this edge must lie on a currently shortest path towards the respective sink. We measure current shortest path length by current waiting times in queues plus physical travel times. For single-sink networks we show existence and termination of IDE flows. For multi-sink networks we show existence and give an example for an instance where IDE flows never terminate.
Talk slides: OMS-Seminar, Arbeitsseminar, IPCO 2019, DCGT 6
Related material: Errata
If you have any questions about my research (or found any mistakes), feel free to contact me. A list of known errata for the above papers can be found here.
Most of my presentations are created using impress.js. You can find the source code for most of them on my gitlab-account.
Since 2023 I am a PostDoc in the group of Tobias Harks at the University of Passau.
From 2017 to 2023 I was a PhD student of Tobias Harks at the University of Augsburg.
I have been a guest on the podcast Algo2Go, where I talked with the hosts Laura Vargas Koch and Niklas Rieken about IDE flows (in German):
Episode 17 - IDEs in dynamischen Flüssen
I am part of the „Mathezirkel-Team“ at Augsburg University - a group of students organizing various activities for pupils interested in mathematics. Some of my lecture notes for such activities can be found here (in German).